Machine Learning Tutorials, Courses and Certifications
Introduction to K-means Clustering¶
K-means clustering is a type of unsupervised learning, which is used when you have unlabeled data (i.e., data without defined categories or groups). The goal of this algorithm is to find groups in the data, with the number of groups represented by the variable K. The algorithm works iteratively to assign each data point to one of K groups based on the features that are provided. Data points are clustered based on feature similarity.
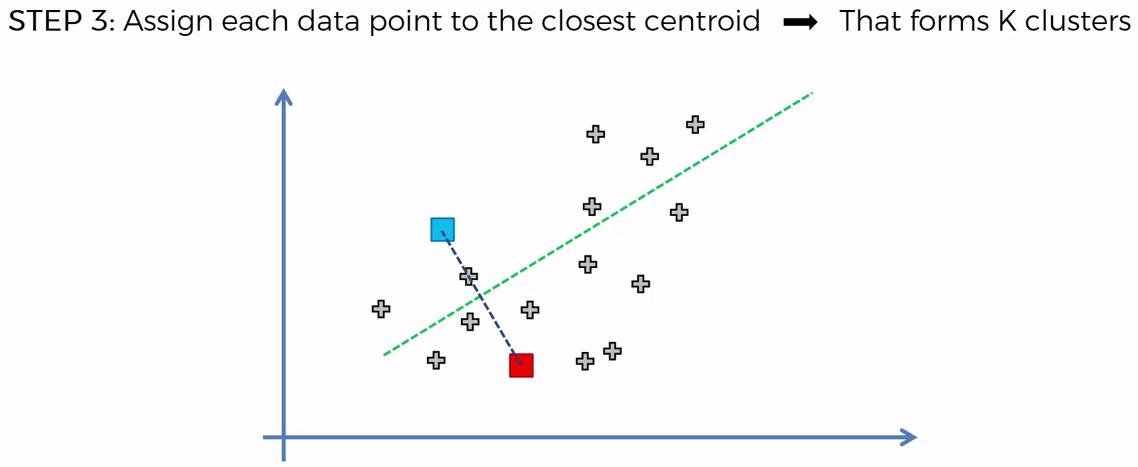
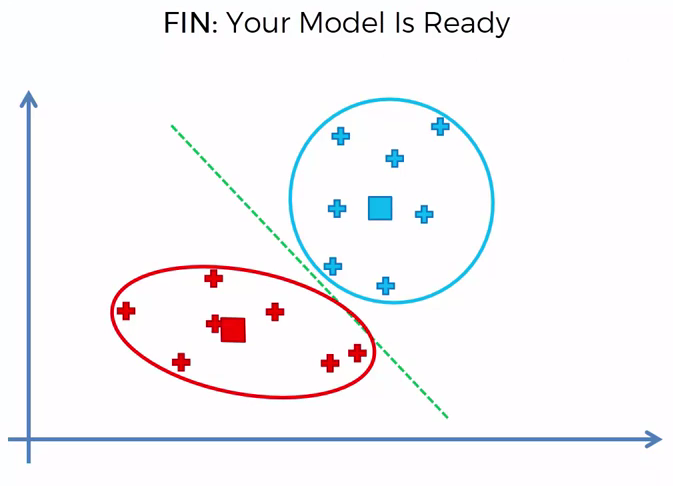
In Simple, It follows a simple procedure of classifying a given data set into a number of clusters, defined by the letter “k,” which is fixed beforehand. The clusters are then positioned as points and all observations or data points are associated with the nearest cluster, computed, adjusted and then the process starts over using the new adjustments until a desired result is reached.
How the K-means algorithm works¶
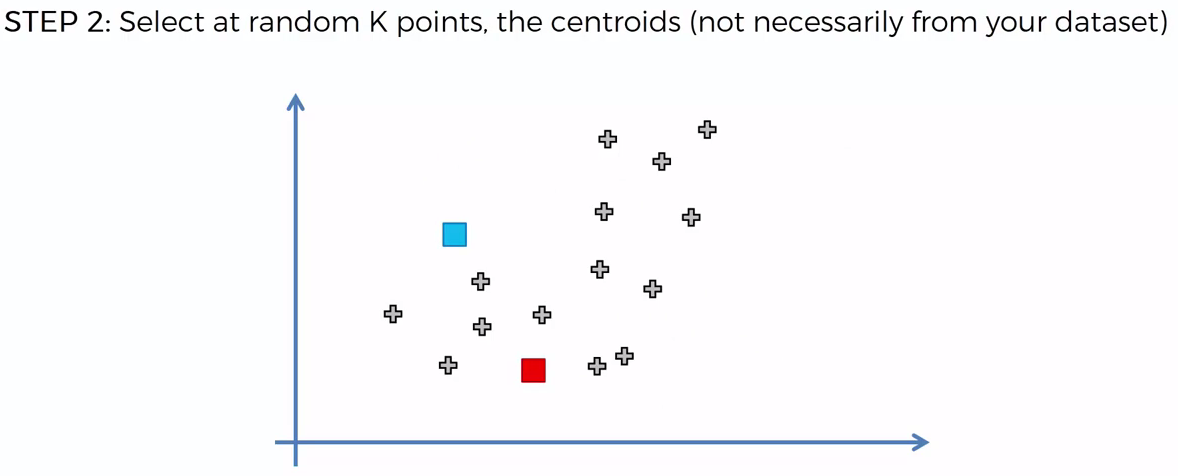
To process the learning data, the K-means algorithm in starts with a first group of randomly selected centroids, which are used as the beginning points for every cluster, and then performs iterative (repetitive) calculations to optimize the positions of the centroids
Business Uses¶
- Behavioral segmentation:
- Segment by purchase history
- Segment by activities on application, website, or platform
- Define personas based on interests
- Create profiles based on activity monitoring
- Inventory categorization:
- Group inventory by sales activity
- Group inventory by manufacturing metrics
- Sorting sensor measurements:
- Detect activity types in motion sensors
- Group images
- Separate audio
- Identify groups in health monitoring
- Detecting bots or anomalies:
- Separate valid activity groups from bots
- Group valid activity to clean up outlier detection
Given Dataset¶
K={2,3,4,10,11,12,20,25,30}
Let say, we want to create two clusters, Take K=2
As we are randomly select the two mean values: Lets cal for Cluster
Step 1:
- M1=4 M2=12
- K1={2,3,4} K2={10,11,12,20,25,30}
Step 2:
- Take the mean for K1 and K2
- M1=3 M2=18
- K1={2,3,4,10} K2={11,12,20,25,30}
Step3:
- Again take the mean for K1 and K2
- M1=4.75 M2=19.6
- K1={2,3,4,10,11,12} K2={20,25,30}
Step4:
- Again take the mean for K1 and K2
- M1=7 M2=25
- K1={2,3,4,10,11,12} K2={20,25,30}
Step5:
- Again take the mean for K1 and K2
- M1=7 M2=25
- K1={2,3,4,10,11,12} K2={20,25,30}
- M1=7 M2=25
As we got the same mean, so we have to stop so our new cluster is :
- K1={2,3,4,10,11,12}
- K2={20,25,30}
Choosing K¶
To find the number of clusters in the data, the user needs to run the K-means clustering algorithm for a range of K values and compare the results. In general, Earlier there is no method for determining exact value of K, but an accurate estimate can be obtained using the following techniques.
One of the metrics that is commonly used to compare results across different values of K is the mean distance between data points and their cluster centroid. Since increasing the number of clusters will always reduce the distance to data points, increasing K will always decrease this metric, to the extreme of reaching zero when K is the same as the number of data points. Thus, this metric cannot be used as the sole target. Instead, mean distance to the centroid as a function of K is plotted and the “elbow point,” where the rate of decrease sharply shifts, can be used to roughly determine K.
Simple Practical to Understand K-Means Clustering Algorithm¶
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
X= -2 * np.random.rand(100,2)
X1 = 1 + 2 * np.random.rand(50,2)
X[50:100, :] = X1
plt.scatter(X[ : , 0], X[ :, 1], s = 50, c = 'r')
plt.show()
Kmean = KMeans(n_clusters=2)
Kmean.fit(X)
print(Kmean.cluster_centers_)
print(Kmean.labels_)
plt.scatter(X[ : , 0], X[ : , 1], s =50)
plt.scatter(-0.75243353, -0.95640447, s=200, c='g', marker='s')
plt.scatter(1.87600534, 2.01533769, s=200, c='r', marker='s')
plt.show()
Kmean.predict([[-3.0,-3.0]])
Our Cluster looks like¶
Let, If we have 1 Cluster¶
Let, If we have 2 Cluster¶
Let, If we have 3 Cluster¶
Practical Example with Real Dataset¶
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('../datasets/Mall_Customers.csv')
X = dataset.iloc[:, [3, 4]].values
dataset
x1=dataset.iloc[:,3]
x2=dataset.iloc[:,4]
plt.xlabel("Annual Income (k$)")
plt.ylabel("Spending Score")
plt.scatter(x1,x2)
plt.show()
# Using the elbow method to find the optimal number of clusters
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 0)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
# Fitting K-Means to the dataset
kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 0)
y_kmeans = kmeans.fit_predict(X)
y_kmeans
# Visualising the clusters
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 100, c = 'red', label = 'Standard')
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Careless')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Target')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 100, c = 'cyan', label = 'Careful')
plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 100, c = 'magenta', label = 'Sensible')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 300, c = 'yellow', label = 'Centroids')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()
